

一次関数(水槽)
【水槽が出てくる一次関数の文章問題】
80リットルで満水となる水槽にすでに17リットルの水が入っています。ここに満水になるまで毎分9リットルの水を入れていきます。水を入れ始めてからx分後の水槽の水の量をyリットルとしたとき、yをxの式で表しなさい。
水槽(すいそう)に水を溜めていくというのは一次関数の定番文章問題のひとつです。
「蛇口が2つ」「排水もしている」などいろいろなパターンの問題がありますが、まずは上の例題で基本となる考え方を覚えておきましょう。
図に書いて整理する
水槽の問題が出たときはカンタンな図を書いてポイントを整理しましょう。
上の例題であれば下記のような図になります。
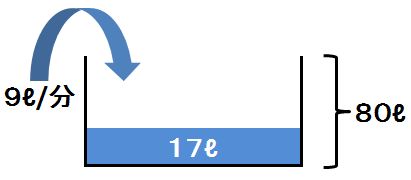
この問題でのポイントは3つです。
- 80リットルで満水
- もともと17リットル入っている
- 毎分9リットルの水が増える
で、問題文から「x」と「y」も整理します。
- 「x」 … 水を入れ始めてから何分後か
- 「y」 … 水槽の水の量
1分後と2分後を考える
まず、水を入れ始めてから1分後の水の量を考えてみます。
「もともと17リットル」あるところに、「毎分9リットル」の水を入れるので、17+9=26リットルとなります。(毎分9リットルとは1分間で9リットルという意味です。)
2分後は、「毎分9リットル」が2分間入ったので、9×2=18リットル。もともとあった17リットルを足すと35リットルとなります。
「x」と「y」を表にすると下記のようになります。
| x分後 | yリットル |
|---|---|
| 1 | 26 |
| 2 | 35 |
| 3 | 44 |
| … | … |
これを式にすれば答えとなります。
式にする考え方
x分後の水の量とは、x分間で増えた水の量+もともと入っていた水の量となります。
水槽から排水されていない場合はこうなります。しっかり覚えましょう。
x分後の水の量 = もともとの水の量 + x分間で増えた(入れた)水の量
「x分後の水の量」とは「y」のことです。
なので、これに数字をあてはめれば「y=…」の式になります。
もともとの水の量は問題文から17リットルとわかります。
x分間で増えた(入れた)水の量も、「毎分9リットルの水が増える」から計算できます。「毎分9リットルの水が増える」とは「1分あたり9リットルの水が増える」という意味です。
- 1分なら9×1=9リットル
- 2分なら9×2=18リットル
- x分なら9×x=9xリットル
x分間で増えた(入れた)水の量とは「9x」となります。
以上で求めたものを下記の式にあてはめたのが答え。
x分後の水の量 = もともとの水の量 + x分間で増えた(入れた)水の量
答え.y=9x+17
(17+9xをxを前にして入れかえています。)



















