中二数学「一次関数：変化の割合の文章題」

 

一次関数の勉強では独特の用語がいくつか出てきます。
「変化の割合」もそのひとつ。

 

「変化の割合を求めよ」と言われても、意味がわからなければ求めようがないですよね。
「増加量」など関連ワードとともに覚えておきましょう。

 

変化の割合とは

 

式にすると次のようになります。

 

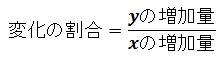
これだと増加量の意味がわからないと意味不明のままですよね。

 

増加量とは、変化した値の量のことです。
例題では「ｘが３から７に増えた」となっています。

 

３から７に増えたので、変化したのは７−３＝４。
この場合の増加量は「４」というわけです。

 

減っていても増加量

注意しないといけないのは変化した値が減っていても増加量ということです。
「ｘが９から２に減った」ときの増加量は２−９＝−７。

 

増加量は「−７」とマイナスがつきます。

この式を覚えておきましょう。

 

例題の解き方

ここまでわかれば例題はカンタンに解けるハズです。

 

まずは、ｘとｙの増加量を求めます。

• ｘの増加量＝７−３＝４
• ｙの増加量＝３−（−５）＝８

マイナスがある場合（例題だとｙ）は符号に気をつけましょう！

 

ｘとｙの増加量がわかればあとは式にあてはめるだけ。

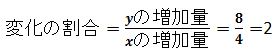
ｘが分母になることを間違えないようにしてください。

 

答え．変化の割合＝２