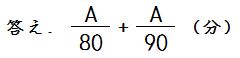中一数学「文字式」での速さに関する問題

 

速さ、時間、距離を文字式で表しなさいというのは定番問題です。
上の例題には、答えに関係のない文字も含まれています。

 

引っかからないように注意して考えましょう。

 

速さの公式はひとつ覚えておけばＯＫ

速さ、時間、距離を求める公式は「は・じ・き」の公式として覚えている人もいるかもしれません。

• 速さ＝距離÷時間
• 時間＝距離÷速さ
• 距離＝速さ×時間

難しくはないのですが、３つ覚えようとするとややこしいですよね。
ウロ覚えだとテストで時間のないときにケアレスミスをしてしまいがちです。

 

速さの公式は３つ覚えるのではなく、１つを確実に覚えましょう。

かけ算なので順番は逆「時間×速さ」でもＯＫ。
距離は、「残りの２つをかける」とだけ覚えれば十分です。

 

これさえ覚えれば、あと２つの公式は導き出せます。

 

例えば、速さを求める公式は「距離＝速さ×時間」から両辺を時間で割ることで求められます。

• 距離＝速さ×時間
• 　⇒　距離÷時間＝速さ×時間÷時間
• 　⇒　距離÷時間＝速さ
• 　⇒　速さ＝距離÷時間

 

時間を求める公式は…

• 距離＝速さ×時間
• 　⇒　距離÷速さ＝速さ×時間÷速さ
• 　⇒　距離÷速さ＝時間
• 　⇒　時間＝距離÷速さ

 

文字式（速さの問題）の解き方

では、上の例題を解いていきます。

 

問題文にはＢ地点とありますが、これは答えに関係のない文字です。
Ｂ地点ではなく、学校でも病院でも駅でも答えは同じです。

 

行きと帰りで速さ（分速）が違うので、それぞれの時間を求めて、それを足したものが往復の時間となります。

 

時間を求める公式は、「距離÷速さ」です。

 

行きの時間は「Ａ÷８０」、帰りの時間は「Ａ÷９０」となります。
これを足したものが往復の時間です。