中一数学「方程式」での速さと距離に関する問題

方程式（距離）

【速さに関する方程式の文章問題（距離）】

駅から湖まで往復するのに行きは時速４ｋｍ、帰りは時速６ｋｍで進んだところ、往復で２時間３０分かかりました。駅から湖までの距離を求めなさい。

速さを変えて往復したときの距離を求めなさいという問題です。
定番問題になっているものですので、解き方を確実に覚えておきましょう。

方程式に関する文章題は何を「ｘ」にするかがポイントとなることがありますが、この問題では悩む必要がありません。問題文で求められている「駅から湖までの距離」を「ｘ」とします。

あとは速さの公式を使って「ｘ」が含まれる式を組み立てます。

【速さの公式】

式を組み立てるために、問題文に着目します。
問題文からわかることは下記。

速さは行きと帰りのそれぞれが与えられているのに対し、時間は往復でしかわかりません。
行きか帰りの時間がわかれば答えはカンタンですよね。

仮に行きに３時間かかったとするなら、行きの時速は４ｋｍなので、距離は４×３＝１２ｋｍ。
帰りの速さなど使わずに問題が解けてしまいます。

これは小学生レベルの問題です。
時間は往復でしかわからないが、帰りの時速がわかるというのが中学生レベルです。

往復の時間＝行きの時間＋帰りの時間

すごくあたり前のことですが、これに気づくのがこの問題を解くカギです。

時間を求めるのに必要なのは「速さ」と「距離」ですよね。

「速さ」は行き、帰りそれぞれ問題文に含まれています。そこで、「駅から湖までの距離」を「ｘ」とすれば行きの時間と帰りの時間を求める式ができます。

この合計が２時間３０分というわけです。

式にすると次のようになります。

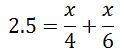
２時間３０分は時間に単位をあわせて２．５となります。

あとはこの式を解くだけ。

３０＝３ｘ＋２ｘ

ｘ＝６となります。

答え（駅から湖までの距離）．６ｋｍ