比例の式と反比例の式のちがい（中一数学）

 

比例の式と反比例の式の違いが分かればカンタンな問題です。
それぞれの式の立て方を思い出しましょう。

 

問題文の「ｙをｘの式で表せ」とは比例、反比例の式を立てろという意味です。

 

 

比例の式の立て方

比例の式にｘとｙをあてはめて比例定数「a」を求めれば、比例の式を立てることができます。

 

問題文では「ｘ＝２のとき、ｙ＝１２となる」とあります。
これをあてはめてみます。

 

となると、「a」はカンタンですね。

• a＝１２÷２
• a＝６

 

これが（１）の答え。

 

なお、比例の場合の比例定数の求め方を覚えていれば、ｘとｙをあてはめなくてもすぐに計算することができます。※『比例の場合の』とあるのは反比例の場合は違うからです。

 

 

反比例の式の立て方

反比例の場合も同様に反比例の式にｘとｙをあてはめて考えます。

 

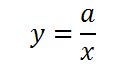
問題文の「ｘ＝２のとき、ｙ＝１２となる」をあてはめて考えると次のようになります。

 

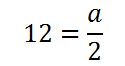
計算すると、

• a＝１２×２
• a＝２４

 

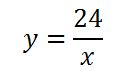
これが（２）の答えとなります。

 

反比例の場合の比例定数の求め方も整理しておきましょう。
なお、反比例でも「反比例定数」ではなく「比例定数」と呼びます。

 

 

反比例は「ｘ」と「ｙ」を掛けた値が比例定数「a」になります。
コレを覚えておけば、問題文の「ｘ」と「ｙ」の値からすぐに比例定数「a」が計算できます。

 

比例の式、反比例の式でのケアレスミスに注意！

上の例題のように同じ「ｘとｙの値」で「比例の式」と「反比例の式」を求めさせる問題でやってしまいがちなミスが「比例の式」と「反比例の式」の比例定数を同じにしてしまうことです。

 

比例の式で比例定数を求めて、それを反比例の式にもあてはめるといったやり方。
比例の式と反比例の式では比例定数が異なります。

 

上の例題で確認してみてください。

• 比例の式の比例定数…６
• 反比例の式の比例定数…２４

違いますよね。
同じだと勘違いしないようにしましょう。