中一数学「反比例の式」に関する基本問題

 

複雑に考えすぎてしまうと、つまづきやすいのが「反比例」です。「何が比例の『反対』なの？」とか反比例の「反」という言葉にこだわりすぎてしまうと深みにはまります。

 

反比例という言葉は置いておいてシンプルにポイントを覚えましょう。

 

これが反比例

反比例に関しては理屈で覚えるよりも式で覚えてしまったほうがカンタンです。

 

 

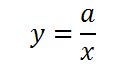
ｘが分母、ａが分子です。
ａは比例定数と呼ばれるもので、ａについて式を変換すると次のようになります。

 

シンプルですよね。
（反比例でも比例定数です。反比例定数ではありません）

 

反比例の式でｘが分子か分母かわからなくなってしまったときは、この式を思い出して変換してみてください。【比例定数ａの求め方】の式の両辺をｘで割ると【ｙがｘに反比例するときの式】です。

 

反比例の式に関する基本問題の解き方

ここまでマスターできれば問題を解くのはカンタンです。

 

まずは、比例定数「ａ」を求めます。
問題文に「ｘ＝−４のときｙ＝１５となる。」とあります。

 

【比例定数ａの求め方】にあてはめると、

• ａ＝−４×１５
• ａ＝−６０

比例定数「ａ」が−６０だとわかります。

 

これで反比例の式を作ると次のとおり。

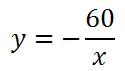
あとは、問題文「ｘ＝１２のときのｙの値を求めよ」をあてはめて計算すればＯＫ。
ｙ＝−５が答えです。

 

答え．ｙ＝−５

 

反比例の式 解き方のキーポイント

反比例の場合は、ｘとｙをかけると比例定数「ａ」が計算できます。算出した比例定数「ａ」を使って反比例の式にｘかｙをあてはめれば、もう一方を求めることができます。

 

反比例の式でｘが分母か分子か思い出せないときは、比例定数ａを求める式「ａ＝ｘｙ」から式を変形すればＯＫです（両辺をｘで割ると反比例の式になります）。