中一数学「反比例の式」での水槽に関する基本問題

 

問題文に水そうが出てくるのは比例の式だけではありません。
反比例の式の文章題でも出題されることがあります。

 

比例のケースと反比例のケースを混同しないように整理して覚えておきましょう。

 

水そう反比例問題の解き方

まず問題文を読むと２つのポイントがわかります。

• 毎分１５リットル水を入れる
• ２０分で水そうがいっぱいになる

この２つから、水そうが何リットルでいっぱいになるかが計算できますね。

 

問題文にある「この水そうがいっぱいになる時間をｙ分」の「この水そう」とは「３００リットルでいっぱいになる水そう」のことだとわかります。

 

３００リットルでいっぱいになる水そうに毎分ｘリットルの割合で水を入れているのだから、３００÷ｘ＝いっぱいになる時間（ｙ分）となります。

 

 

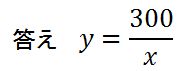
カンタンでしたよね。

 

水そう「反比例問題」のポイント

水そうが出てくる反比例問題で多いのは上記のパターン。
「毎分●●の割合で水を入れると、▲▲分でいっぱいになる」というもの。

 

このケースでは次の公式を覚えておきましょう。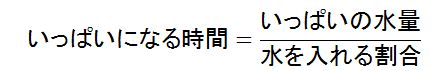

 

「いっぱいの水量」とは、水そうがいっぱいになったときの水の量のこと。
「水を入れる割合」は毎分●●リットルの割合で水を入れるのことです。

 

いっぱいになる水量は変わらない（水そうの大きさにより決まる）ので、変化するのは『時間』と『割合』。

 

『時間』を短くしたいなら、『割合』を大きくする必要があります。

 

毎分あたりの入れる水の量を多くすれば、いっぱいになる時間が短くなるというわけです。感覚的に考えてもわかりますよね。

 

このことを感覚ではなく式で表したのが上の反比例の式というわけです。

 

覚えておいて、使いこなせるようになりましょう。