中二数学「公式を覚えずに組合せの数を求める問題を解く方法」

「７枚のカードから５枚のカードを選ぶときの組み合わせの数を求めよ」のような組み合わせの数を求める問題は公式を使って解くことができます。

 

 

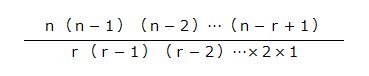
「７枚のカードから５枚のカードを選ぶ」にあてはめると次のようになります。

 

あとは計算するだけ、分母と分子にある「５×４×３」が約分できるので計算は難しくないのですが、公式自体はややこしいですよね。ｎとかｒとか出てきちゃうし。

 

実は、中学数学レベルであれば、公式を覚えていなくても解くことができる問題が少なくありません。その方法を紹介します。

 

公式を使わずに組合せの数を求める問題を解く方法

上で紹介した問題（「７枚のカードから５枚のカードを選ぶときの組み合わせの数を求めよ」）は、７チームで総当たりリーグ戦を行うときの試合数と同じになります。

 

総当たりリーグ戦の試合数の求め方は覚えてますか？

 

７チームだと下記のようになります。

 

組合せの数を求める公式で計算したのと同じ結果になります。

 

偶然ではありません。
ポイントとなるのは「２」。

 

リーグ戦の試合数は７チームの中から２チームの組み合わせ数を考えるのと同じです。

 

「７枚のカードから５枚のカードを選ぶ」では、残りが７−５で２となっているのがポイント。
選ばれていない２枚のカードの組み合わせ数＝選んだ５枚のカードの組合せ数です。

 

下の２つの図を見比べてみるとわかります。

 

 

「７枚のカードから５枚のカードを選ぶ」組合せ

 

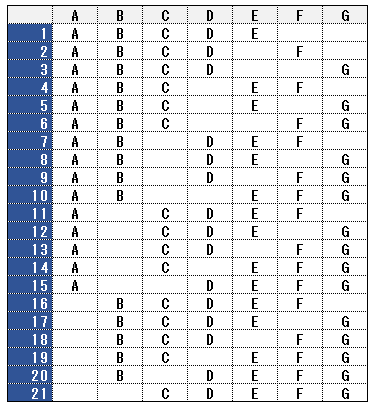
７チームのリーグ戦数

 

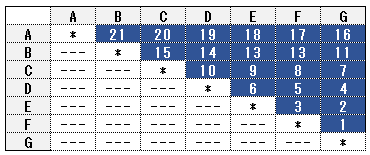
残りが２となる組合せ数を求める問題で使える

• ７枚の中から５枚を選ぶ
• ８個の中から６個を選ぶ
• ３０人の中から２８人を選ぶ

など残りが「２」となるときは、上のようにリーグ戦の試合数を求める方法で計算できます。

 

「そんなに都合よく残りが２になるかよ」と思うかもしれませんが、中学数学レベルであれば、こうした都合の良い数字の問題がかなり出題されています（手元の問題集にも複数あり）。

 

「３０人の中から２８人を選ぶ」なんて公式にあてはめようとすると、３０×２９…と計算がややこしくなります。「リーグ戦方式」で計算できることを覚えておきましょう。