中三数学「素因数分解のやり方と応用問題の解き方解説」

素因数分解のやり方

素因数分解のやり方を覚える前に、まず素数について知らなければなりません。
まずは、定義を確認しましょう。

【素数とは】
素数とは、１と自分の二つしか約数を持たない自然数（１は素数ではない）。

約数というのは割り切れる数のことです。

例えば、４は１と自分（４）以外にも２で割りきれます。
なので、４は素数ではありません。

一方、５は１と自分（５）以外では割り切れません。
なので、５は素数です。

１から１００までだと素数は全部で２５個あります。
下の図の赤字（２，３，５，７，１１…）が素数です。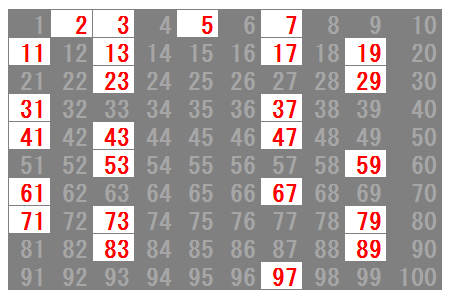

素因数分解とは、その数を素数の積（かけ算）で表すことです。
「１００を素因数分解せよ」とは、「１００を素数のかけ算で表せ」という意味です。

素因数分解のやり方は、素数で割っていくことで行います。
例題で見てみます。

【例題】８４０を素因数分解せよ。

８４０を素数で割り、その答えをまた素数で割ります。
できるだけ小さい素数で割るようにします。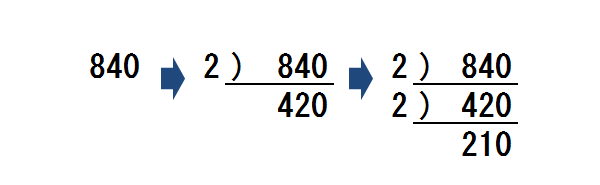

割れなくなるまで（最後が素数になるまで）コレを続けます。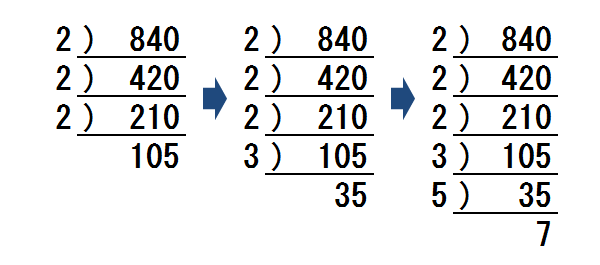

「割った数すべて」と「最後の答え（ここでは７）」のかけ算が答えとなります。

答え．２³×３×５×７

素因数分解で間違いやすいのは、まだ割れるのに割るのをやめてしまうケースです。
それでは正解になりません。

これを見極めるポイントは最後の答えが素数かどうかということ。
素数なら、もう割り切れませんが、素数以外なら割り切れます。

この見極めができるようになるためには、素数を覚えておく必要があります。
中学数学で取り扱う素数は、だいたい１００までぐらいです。

１００までの素数表（下記）で覚えておきましょう。

１００までと言っても、よく出るのは２９ぐらいまでです。
暗記しておきましょう。

素因数分解を利用した典型的な応用問題に次のようなものがあります。

【問題】
２５２に自然数ａをかけたら、ある別の自然数の平方となった。
最も小さい自然数ａを求めよ。

この問題は素因数分解を利用して解くことができます。
まず、２５２を素因数分解します。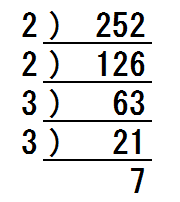

２５２＝２²×３²×７

２５２には、６（２×３）の平方があり、残っているのは７です。
これを平方にするには７をかければ良いことがわかります。

答え．７

（補足）２５２×７＝１７６４で４２の平方（４２×４２）となります。