因数分解での共通因数と二乗数の見つけ方

因数分解での共通因数と二乗数の見つけ方

中三数学の文章題の解き方

因数分解での共通因数と二乗数の見つけ方

因数分解のときに必要な共通因数と二乗になっている数の見つけ方の解説です。

 

共通因数による因数分解

因数分解の最初に出てくるのが「共通因数でくくる」という公式です。

【問題】次の式を因数分解せよ。
３ａ＋９ｂ＋２１

この場合、３が共通因数となるので、３をカッコの外に出します。

【解答】３（ａ＋３ｂ＋７）

 

必要なのは数字の最大公約数をみつけること

共通因数による因数分解で必要なのは数字の部分の最大公約数をみつけることです。
因数分解の前の単元が、素因数分解になっているのはこのためです。

 

素因数分解を使うことで、最大公約数を見つけることができます。
ただし、すべての数字を素因数分解していたのでは時間がかかってしまいます。

 

そこで、代表的な数字同士の最大公約数は覚えておくのが速く解くコツです。
暗記しなくても下記の早見表を眺めておけば、テスト中のひらめきにつながります。

 

表を眺めて、自分が見落としてしまいがちなところをチェックしておきましょう。

 

最大公約数早見表

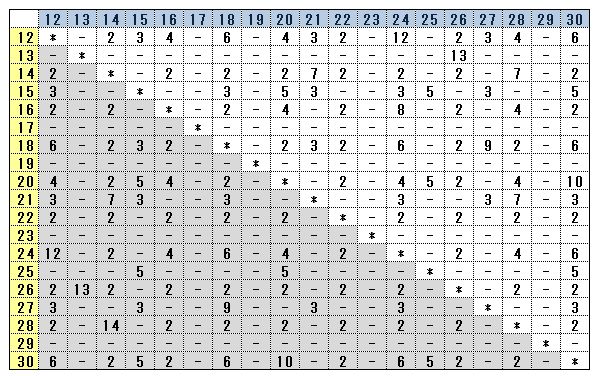
最大公約数早見表
グレーになっている部分は同じ組み合わせがあるところです。

 

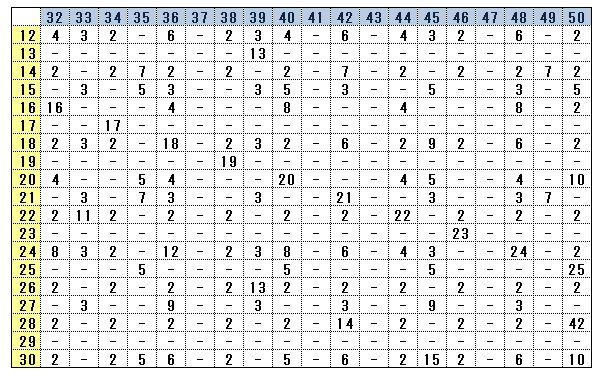
最大公約数早見表32-50
３１は、１２から３０には１より大きい最大公約数がないので省略しています。

 

二乗による因数分解

因数分解の公式に「二乗−二乗」があります。

【因数分解の公式】
ａ²−ｂ²＝（ａ＋ｂ）（ａ−ｂ）

例えば下記のような問題です。

【問題】次の式を因数分解せよ。
ａ²−２５

２５が５の二乗なので、答えは次のようになります。

【解答】（ａ＋５）（ａ−５）

 

二乗の数を見つける

この問題を解くには数字が何かの数の二乗かどうかを判断しなければなりません。
まずは１から２０までを二乗した数を覚えておきましょう。

 

この数字にピンとくる感覚を持っておくことが大切です。

 

１から２０までの二乗数

二乗数 元の数 二乗数 元の数
1 1 121 11
4 2 144 12
9 3 169 13
16 4 196 14
25 5 225 15
36 6 256 16
49 7 289 17
64 8 324 18
81 9 361 19
100 10 400 20

 

下１ケタから何の二乗かを推測する

上では２０までの二乗数を掲載しましたが、大きな数になったときに知っておくと便利な法則があります。下一桁の数字で、何の二乗の可能性があるかが決まっているのです。

 

自然数の場合にあてはまる法則です。中学の数学ではこれで十分です。

 

下一桁が１の数字は、下一桁が１か９の二乗

二乗数 元の数 二乗数 元の数
1 1 81 9
121 11 361 19
441 21 841 29
961 31 1521 39
1681 41 2401 49
2601 51 3481 59
3721 61 4761 69
5041 71 6241 79
6561 81 7921 89
8281 91 9801 99
10201 101 11881 109

 

必ずなるわけではない

下一桁が１の数字は必ず下一桁が１か９の二乗になるわけではありません。
二乗になるなら元の数の下一桁は１か９という意味です（以降も同じ）。

 

下一桁が４の数字は、下一桁が２か８の二乗

二乗数 元の数 二乗数 元の数
4 2 64 8
144 12 324 18
484 22 784 28
1024 32 1444 38
1764 42 2304 48
2704 52 3364 58
3844 62 4624 68
5184 72 6084 78
6724 82 7744 88
8464 92 9604 98
10404 102 11664 108

 

下一桁が６の数字は、下一桁が４か６の二乗

二乗数 元の数 二乗数 元の数
16 4 36 6
196 14 256 16
576 24 676 26
1156 34 1296 36
1936 44 2116 46
2916 54 3136 56
4096 64 4356 66
5476 74 5776 76
7056 84 7396 86
8836 94 9216 96
10816 104 11236 106

 

下一桁が９の数字は、下一桁が３か７の二乗

二乗数 元の数 二乗数 元の数
9 3 49 7
169 13 289 17
529 23 729 27
1089 33 1369 37
1849 43 2209 47
2809 53 3249 57
3969 63 4489 67
5329 73 5929 77
6889 83 7569 87
8649 93 9409 97
10609 103 11449 107

 

下二桁が２５の数字は、下一桁が５の二乗

二乗数 元の数
25 5
225 15
625 25
1225 35
2025 45
3025 55
4225 65
5625 75
7225 85
9025 95
11025 105

 

整理すると次のようになります。

二乗の数の見つけ方

  • 二乗数下一桁が　１→　元の数の下一桁は１か９
  • 二乗数下一桁が　４→　元の数の下一桁は２か８
  • 二乗数下一桁が　６→　元の数の下一桁は４か６
  • 二乗数下一桁が　９→　元の数の下一桁は３か７
  • 二乗数下二桁が２５→　元の数の下一桁は５
  • 上記以外の下一桁２，３，７，８は、自然数の二乗にはならない