

「場合の数」で間違いやすい問題はコレ
中学2年数学の確率の単元の最初にならうのが「場合の数」です。
この「場合の数」には定番の間違いやすい引っかけ問題があるので気をつけましょう。
まずは「引っかけ」じゃないノーマルな問題から確認します。
場合の数の基本問題
【問題−1】
1,2,3から数字を2つ選んでできる2ケタの数字は何通りありますか?(ただし、同じ数字を2つ選ぶことはできません)
これが教科書でも最初のほうに出てくる場合の数の問題です。
樹形図を使って整理すると次のようになります。

1,2,3の3つの数字なので、最初の数字は3通り。
同じ数字を2つ選ぶことはできないので、2番目に選ぶ数字は2通りずつ。
3通り(最初の数字)×2通り(次に選ぶ数字)=6通り が答えとなります。同じ数字を選べないので、2番目の数字が「最初の数字の組合せ数−1」となるのがポイント。
数が多くて樹形図を書くのが大変なときは、計算式にあてはめて解きます。
練習してみましょう。
【問題−2】
1,2,3、4,5,6,7,8,9までの数字を2つ選んでできる2ケタの数字は何通りありますか?(ただし、同じ数字を2つ選ぶことはできません)
最初の数字は9通り(1から9まで)。
次の数字は8通り(9通り−1)。
よって、答えは9×8=72通りとなります。
次が引っかけ問題です。
場合の数のひっかけ問題
【問題−3】
0,1,2,3,4から数字を2つ選んでできる2ケタの数字は何通りありますか?(ただし、同じ数字を2つ選ぶことはできません)
最初の数字は5通り(0から4まで)。
次の数字は4通り(5通り−1)。
よって、答えは5×4=20通り とするのは間違いです。
ゼロに注意!
「01」「02」など十の位が「0(ゼロ)」となるのは2ケタの数字はありません。
つまり、上の問題では最初の数字に「0(ゼロ)」を選ぶことはできないのです。
最初の数字として考えられるのは、「1,2,3,4」の4通り。
じゃぁ、次の数字は3通り(4通り−1)。とするのも間違い!
次の数字(2番目の数字には0が来てもOKです。)
「10」「20」は2ケタの数字ですよね。
なので、2番目の数字の組み合わせは4通りです。
よって、答えは4×4=16通りとなります。
表で整理すると次のようになります。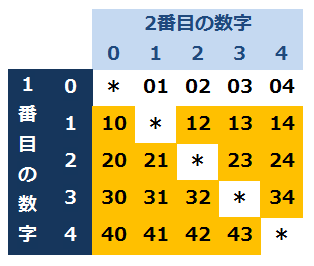
色のついているところが2ケタの数字です。
場合の数の「数字を作れ問題」で「0(ゼロ)」が出てきたら要注意!