連立方程式の問題（橋やトンネルを通る電車の速さと長さ）

連立方程式の文章題に橋やトンネルを通る電車の速さと長さを求める問題があります。
（中学２年数学の範囲）

 

この問題の解き方と間違いやすいポイントを解説します。
まずは、問題から見てみましょう。

 

 

長い文章題を解くには、ポイントを書き出すのがコツです。

	橋	トンネル
長さ	１１５０ｍ	１６００ｍ
通過時間	４３秒	５８秒

問題文を整理するとこうなりますね。
で、求めるべきものは電車の速さ（秒速）と長さです。

 

橋（トンネル）の長さ＋電車の長さから速さを求める

電車が橋やトンネルを通過する問題の最大のポイントは、通過した時間から速さを求めるときに、橋やトンネルの長さだけではなく、電車の長さも含めて考えなければならないことです。

 

問題文には「橋を渡り始めてから、渡り終わるまで」とあります。

• 「橋を渡り始めた」ときは、電車の先頭が橋に入っている状態です。
• 「橋を渡り終えた」ときは、電車の最後尾が橋から出た状態です。

 

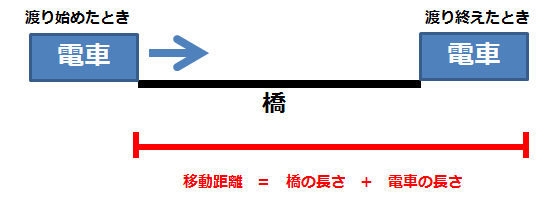
問題文にあてはめると、この移動距離を43秒で通過したことになります。
トンネルに入る、出るも同じように考えます。

 

求めるものをＸとＹにする

連立方程式の文章題では求めるものをＸとＹにします。
この問題では次のようになります。

• Ｘ＝電車の速さ（秒速）
• Ｙ＝電車の長さ

このＸとＹを用いて、問題文から式を作ります。
そのときに、上記で説明した「移動距離」を間違えないようにするのがポイントです。

 

この部分を式にすると次のようになります。
「長さ　÷　速さ　＝　時間」の式を使います。

 

こちらも同じように式にします。

 

式が立てられれば、あとは連立方程式を解くだけです。

 

答え．秒速３０ｍ、長さ１４０ｍ